By Bob Reselman
For as long as there’s been an internet, there have been security threats. Fortunately the good guys have been able to come up with ways to meet the growing number of hazards. But, this has come with a performance price. Until the introduction of Transport Layer Security (TLS) 1.3, doing something as simple as a “Hello World” between browser and website required a number of requests and response round trips to establish a secure connection.
Security protocols have evolved a great deal since Netscape released Secure Sockets Layer (SSL) in 1995. Unfortunately SSL had some significant security vulnerabilities that in 2014 led the US Government to restrict its use on websites exchanging HIPAA data and sensitive government information. Instead, the government mandated the use of the next generation security protocol, Transport Layer Security (TLS).
TLS addressed the security vulnerabilities in SSL, but TLS versions before 1.3 still had the performance problem incurred by the extended handshake. Under TLS 1.2, the connection handshake required at least a 2 request-response exchange to authenticate a client to the server.
Today, TLS 1.3 has reduced the key creation handshake to a single request and response round trip. That single round trip makes it possible for both the client and server to share the same encryption key. But, that encryption key never travels over the internet. Rather, the key is created independently on the client and server simultaneously, using a technique called the Diffie-Hellman key exchange. The key is created “just in time”. The term used to describe the process is called “ephemeral key exchange.”
Sharing the details of working with ephemeral key exchange under TLS 1.3 is the purpose of this article. I am going to go into exacting detail about the mechanics of Diffie-Hellman. There are a few mathematical formulas involved, which I will cover. Also, in order to provide more clarity, I have added a bonus appendix that inserts actual numbers into the Diffie-Hellman formulas. You can see the actual calculations and their results in this appendix.
Before we dive in, please be advised that Diffie-Hellman key exchange does have some security vulnerabilities. I will discuss these vulnerabilities at the end of the article. Yet, despite its shortcomings, Diffie-Hellman implements data encryption in a manner that is worth noting. Unlike the public key exchange between client and server that is intrinsic to public/private key encryption, under Diffie-Hellman, the exchange of a key that is used for encryption never travels over the internet. The details of the technique will be revealed in the sections that follow.
Understanding the TLS 1.3 Handshake and Key Creation
As mentioned above, one of the ways that TLS 1.3 can encrypt data is to make it so both the client and the server have the capability to encrypt data using the same private key. But, that private key is never exchanged over the internet. The way it works is that both client and server create their own secret key value. The client has a unique secret key value. The server has a unique secret key value. The client and server will use their respective secret key values in conjunction with a public key that is known to both, in order to create the ephemeral symmetric key.
This public key is made up of a very large prime number, p, and base value, g, that is a primitive root. The concept of primitive root comes from the field of modulo arithmetic. A primitive root is an integer that is special in the way that it relates to remainders when dividing one number by another. (Primitive root is not a particularly complex concept, but it does take some time to understand — time, unfortunately, that is beyond the scope of this article.) The important thing to understand about using a big prime number and primitive root together as a public key is that it creates a mathematical relationship that is suited well to the Diffie-Hellman key exchange technique.
Let’s pause a moment to do a short review, before going further with particulars of ephemeral key encryption.
As it now stands when it is time to do a secure data exchange using an ephemeral, symmetric key, both the client and the server will create a special secret key value independently. This secret key value is a random number particular to each party. Also, both client and server will share a public key composed of a very big prime number and a number that is a primitive root. That the public key is exposed on the internet is not particularly troubling because, as strange as it sounds, its value is only useful within the distinct privacy of the client on one hand and the distinct privacy of the server on the other.
Now let’s move to the client side of things and examine the creation of the secret key.
On the client side, the client will apply the prime number and the primitive root defined in the public key along with the private, random value number, to create a secret key using a special mathematical formula. Listing 1 below shows the formula used to create the secret key value, which is represented by the variable, A.
| A = ga mod p
WHERE
|
Listing 1: The formula the client uses to create a temporary key value to send to the server
The client then sends that number A to the server.
On the server side, the server executes the formula as the client did, in this case creating a secret key, B. But the server will use its private random number b, as shown below in Listing 2.
| B = gb mod p
WHERE
|
Listing 2: The formula the server uses to create a temporary key value to send to the client
The server will send the number, B to the client.
Where it stands now is that the server has the client’s temporary value A, and the client has the server’s temporary value B. Figure 1, below illustrates the dynamics behind the secret key generation and exchange. (The figure also shows how the symmetric private key is generated. But, let’s not get too far ahead of ourselves.)
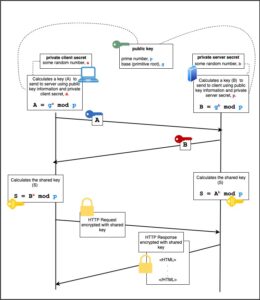
Figure 1: Under Diffie-Hellman data encryption both client and server use a private key that’s never exchanged.
After the secret key exchange takes place, both the client and the server will generate the shared private key that both parties will use to encrypt and decrypt data.
Generating the shared private key is facilitated with another formula that is used similarly by both the client and server. Listing 3 below shows the formula used by the client to create the private key.
| S = Ba mod p
WHERE
|
Listing 3: The formula used by the client to generate the private key shared with the server
Listing 4 below shows the formula used by the server to create the shared private key.
| S = Ab mod p
WHERE
|
Listing 4: The formula used by the client to generate the private key shared with the server
The result of the client executing the formula shown above in Listing 3 and the server executing the formula shown above in Listing 4 is that they both will end up with the same private key. Thus, both client and server are now capable of exchanging encrypted data using a symmetric key.
(If you want to get a more detailed look at the mechanics of Diffie-Hellman and ephemeral keys, take a look at the appendix provided at the end of this article. It demonstrates creating a symmetric private key under Diffie-Hellman using real numbers.)
Ephemeral, symmetric key encryption is almost magical in a way. No identical keys, public or private, ever travel over the internet.
In order for hackers to create the private key, they would have to get the private random number generated by the client and the private random number generated by the server. This means actually hacking into the client and server machines at the time of the data exchange. Or, somehow the hacker would need to figure out through trial and error, the very big random number used as secret key values on the client and server.
No Encryption Technique is Perfect
Of course, as we have learned in the real world of cybersecurity, if a hacker has enough time and money, nothing is really impossible. Due mostly to its dependence on using a large prime number at random, Diffie-Hellman is one of those techniques that can be hijacked by nefarious actors that have the time, expertise and resources to crack the cipher.
The important thing to understand about hacking Diffie-Hellman is that bad guys of this nature work at the nation-state level, the place where cyber warfare takes place. Breaking Diffie-Hellman requires industrial strength resources. It is typically not something a bored teenager can do as an after-school prank.
Still, history has shown that there is always a new threat at hand, no matter how perfect we might think an encryption technique is. Even the RSA encryption method, which has wide use as an alternative to Diffie-Hellman, has vulnerabilities. As of this writing, many in the industry are suggesting to switch the use of Diffie-Hellman to (Elliptic Curve) Diffie-Hellman or Fully Hashed MQV. Yet, these alternatives are not hack-proof either. As disagreeable as it may seem, sometimes “really good” is all we get, no matter how much we desire perfection.
Putting It All Together
In this article I gave you a fairly in-depth look at the way TLS 1.3 implements ephemeral symmetric key encryption using only one request/response pair. Be advised that although encryption techniques are important, data exchange security is only one part of the picture. TLS supports a number of encryption protocols. Then there is the matter of TLS certificates, as well as support by the various browser and internet servers.
TLS 1.3 is a very big topic. But, hopefully, the advantages of single round trip handshakes and ephemeral session keys discussed herein will help shed some light on a good size portion of the TLS 1.3 protocol.
Appendix: An example of generating an ephemeral key using real numbers
The following is a demonstration of generating a symmetric key shared between client and server as illustrated in Figure 3 above. The example uses real numbers in place of variable placeholders.
| Public key values | Client side secret random number | Server side secret random number |
| Prime number, p = 17
Base (primitive root) g = 3 |
Client random number, a = 11 | Server random number, b = 15 |
Client side generation of key sent to server
| A = ga mod p
Where:
Calculation: 311 mod 17 = 177147 mod 17 177147 mod 17 = 7 |
Server side generation of key sent to client
| B = gb mod p
Where:
Calculation: 315 mod 17 = 14348907 mod 17 14348907 mod 17 = 6 |
Client generates the shared private key
| S = Ba mod p
Where:
Calculation: 611 mod 17 = 362797056 mod 17 362797056 mod 17 = 5 |
Server generates the shared private key
| S = Ab mod p
Where:
Calculation: 715 mod 17 = 4747561509943 mod 17 4747561509943 mod 17 = 5 |
Notice that the value of the key generated by the client and the server independent of each other is 5. Hence, 5 is the value of the shared private key that will be used to encrypt and decrypt data in an exchange between client and server on the internet.
To learn more about secure development practices, Linux Foundation Training & Certification, in partnership with the Open Source Security Foundation (OpenSSF), offers a free series of three online training courses covering Secure Software Development: Requirements, Design, and Reuse (LFD104x), Implementation (LFD105x), and Verification and More Specialized Topics (LFD106x).
This article was originally published at TheNewStack.

